Embedding 是什么
人类可以直接理解现实世界的对象,如文本、图像和音频等,而机器只能够处理数值数据,无法理解这些对象。为了能够让机器进行理解,必须先将它们转化为数值形式。Embedding 就是将现实对象表示为连续向量空间中的点的方法,这些点在空间中的位置蕴含着对象的信息。
具体在 NLP 领域中,词嵌入(Word Embedding)就是将单词转化为数值向量,且向量的相对位置反映了词之间的语义相似性和关系。假设有以下 embedding 后的结果:
- cat:[0.2, -0.4, 0.7]
- dog:[0.6, 0.1, 0.5]
- apple:[0.8, -0.2, -0.3]
- orange:[0.7, -0.1, -0.6]
- happy:[-0.5, 0.9, 0.2]
- sad:[0.4, -0.7, -0.5]
一共 6 个单词,每个单词转化成维度为 3 的向量,进而可以通过计算向量之间的余弦相似性来判断单词的相似度:
$$\begin{aligned} \text{cosine\_similarity(cat, dog)}&=0.66, \\ \text{cosine\_similarity(cat, apple)}&=0.04. \end{aligned}$$猫和狗都是动物,余弦相似性达到 0.66,而猫和苹果几乎没有任何关系,余弦相似性只有 0.04。
Word2Vec
Word2Vec 有两个用于生成词向量的模型:CBOW(Continuous Bag of Words) 和 Skip-gram。
1.CBOW 通过给定窗口中的上下文单词来预测中心单词。

2.Skip-gram 以中心单词为输入,预测给定窗口的上下文单词。

以 Skip-gram 为例,模型使用只有一个没有激活函数的隐藏层的神经网络来训练,由于输入和输出都是离散的单词,可以使用独热编码(One-hot)来表示,神经网络的结构如下:
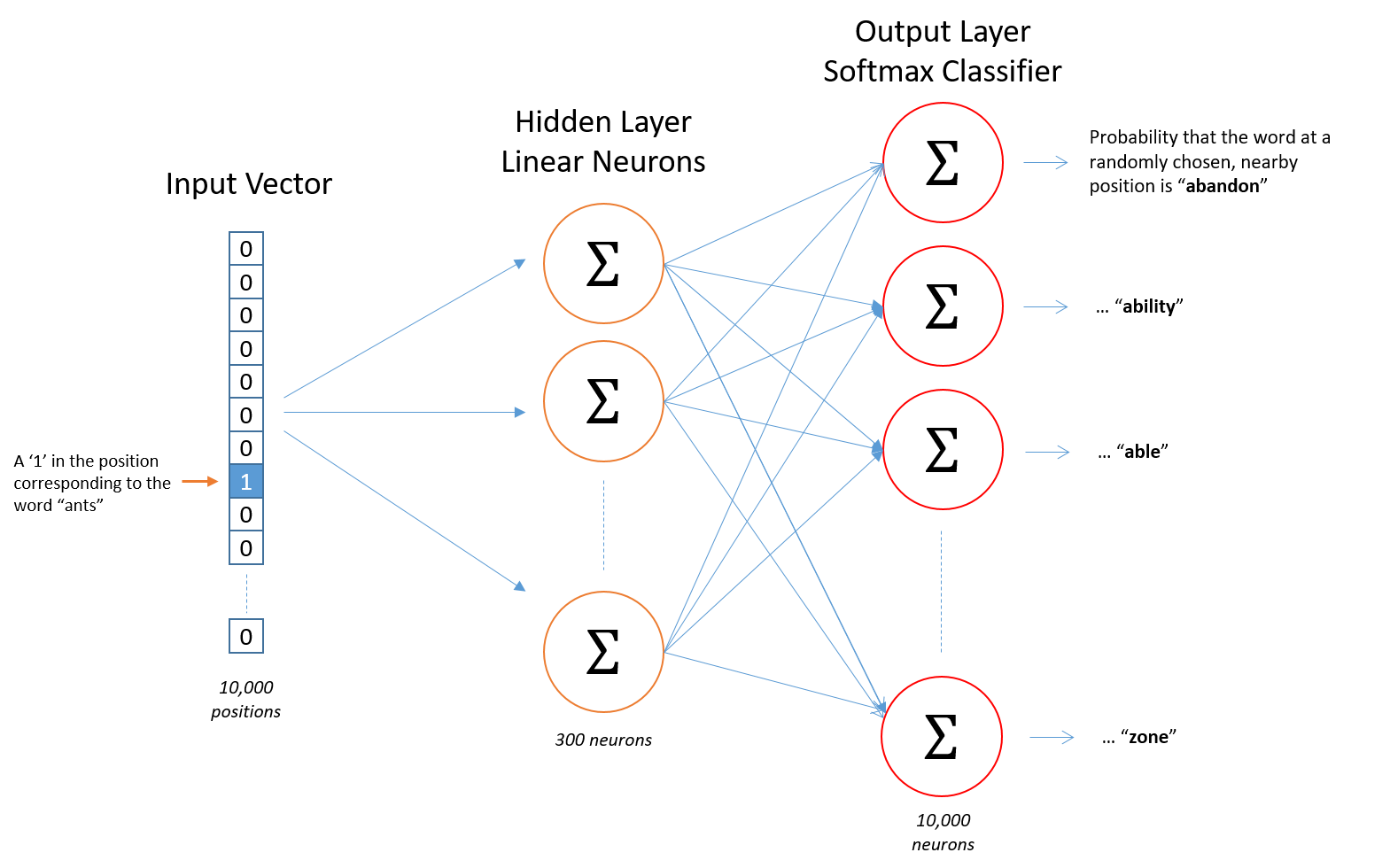
假设词库大小为 10000,embedding 的大小是 300,输入单词“ant”是一个1\(\times\)10000 的向量,经过 softmax 的输出层也是一个 1\(\times\)10000 的向量,它的每个分量表示各个单词的概率。因此,输入层到隐藏层的 embedding 权重矩阵大小为 10000\(\times\)300,隐藏层到输出层的权重矩阵大小为 300\(\times\)10000。通过反向误差传播更新参数,即可得到 embedding 矩阵,每一行对应的就是各个单词的向量表示。
可以看到,神经网络每一层都要训练 300\(\times\)10000=3M 个参数,并且需要大量的训练数据防止过拟合,这意味着训练过程将非常缓慢,效率很低。Word2Vec 的作者在第一篇文章中提出使用 hierarchical softmax 来提高效率,而第二篇文章中提出了另外两个策略来解决这个问题。
1.Subsampling of frequent words
在一段英文文本中,“the”、“in”和“a”这类单词与很多单词同时出现,它们通常不能够给我们提供许多上下文信息。也就是说,这种频繁使用的单词的向量表示在成千上万的样本训练中变化很小。
作者提出了一种 subsampling 策略来解决这个问题,训练集中的每个单词都以一定的概率被丢弃:
$$P(w_{i})=1-\sqrt{\frac{t}{f(w_{i})}}.$$其中,\(f(w_{i})\) 是单词 \(w_{i}\) 出现的频率,\(t\) 是一个阈值。单词出现频率越高,越有可能被丢弃。
2.Negative sampling
输出是一个 1\(\times\)10000 的概率向量,这导致隐藏层到输出层的权重矩阵很大。由于只关心输出是否为正确的单词,因此将标签设置为 1(正确)和 0(错误),模型接受训练集的输入词和输出词,输出一个衡量输入词和输出词是否匹配(属于同一个上下文窗口)的分数。具体地,计算输入词和输出词两个 embedding 向量的点积,再经过 sigmoid 转化为 0-1 之间的数。
但这样还有一个问题,训练样本的标签全都是 1,只要令模型的输出始终为 1,则正确率就有 100%,这是毫无意义的。因此,对于每一个正样本,都从预料库中选取一些单词作为负样本(小数据集 5-20 个,大数据集 2-5 个),原论文采取的负样本单词选取的概率公式为:
$$P(w_{i})=\frac{f(w_{i})^{\frac{3}{4}}}{\sum_{j=0}^{n}f(w_{j})^{\frac{3}{4}}}.$$模型训练时,每次仅对一个正样本及其对应的几个负样本更新参数,假设每个正样本选取 5 个负样本,那么隐藏层到输出层的参数为 6\(\times\)300=1800,远远小于原来的 3M 个参数。
GloVe
GloVe 引入共现矩阵(Co-occurrence Matrix),矩阵的每个元素表示两个单词同时出现在一个上下文窗口的次数。假设语料库有两句话,分别是“I love you.”和“I fall in love with you.”,窗口长度为 2,那么共现矩阵如下:
| I | love | you | fall | in | with | |
|---|---|---|---|---|---|---|
| I | 0 | 1 | 1 | 1 | 1 | 0 |
| love | 1 | 0 | 2 | 1 | 1 | 1 |
| you | 1 | 2 | 0 | 0 | 0 | 1 |
| fall | 1 | 1 | 0 | 0 | 1 | 0 |
| in | 1 | 1 | 0 | 1 | 0 | 1 |
| with | 0 | 1 | 1 | 0 | 1 | 0 |
共现矩阵 \(X\) 的每一个元素 \(X_{ij}\) 表示单词 \(w_{j}\) 出现在单词 \(w_{i}\) 窗口的次数,用频率近似概率,则单词 \(w_{j}\) 出现在单词 \(w_{i}\) 窗口的概率为 \(P_{ij}=P(j|i)=\frac{X_{ij}}{\sum_{k}X_{ik}}=\frac{X_{ij}}{X_{i}}\)。
下面我们来探索如何从共现概率挖掘单词的意义。GloVe 原论文给了如下共现概率表格:
| Probability and Ratio | k=solid | k=gas | k=water | k=fashion |
|---|---|---|---|---|
| \(P(k\|ice)\) | \(1.9\times 10^{-4}\) | \(6.6\times 10^{-5}\) | \(3.0\times 10^{-3}\) | \(1.7\times 10^{-5}\) |
| \(P(k\|steam)\) | \(2.2\times 10^{-5}\) | \(7.8\times 10^{-4}\) | \(2.2\times 10^{-3}\) | \(1.8\times 10^{-5}\) |
| \(P(k\|ice)/P(k\|steam)\) | \(8.9\) | \(8.5\times 10^{-2}\) | \(1.36\) | \(0.96\) |
“solid”与“ice”相关,与“steam”不相关,故共现概率之比 Ratio 较大,为 8.9;“gas”与“ice”不相关,与“steam”相关性强,Ratio 仅仅为 0.085;“water”与“ice”和“steam”的相关性都比较强,“fashion”与“ice”和“steam“几乎不相关,Ratio 都接近于 1。因此单词之间的关系可以通过 Ratio 来反映,进而通过这个关系学习词向量,这是 GloVe 的核心思想。
基于上述思想,假设词向量 \(w_{i},w_{j},w_{k}\) 通过某个函数 \(F\) 的作用,呈现出与 Ratio 一致的规律和信息:
$$F(w_{i},w_{j},w_{k})=\frac{P_{ik}}{P_{jk}}.$$词向量空间是线性的,且三个单词是可以互相转换的,不妨考虑 \(w_{i}\) 和 \(w_{j}\) 之间的关系,最简单的关系就是 \(w_{i}-w_{j}\),因此
$$F(w_{i}-w_{j},w_{k})=\frac{P_{ik}}{P_{jk}}.$$由于等式左边函数作用在向量上,而等式右边是一个标量,为了保证等式能够成立,可以使用向量点积将向量转化为标量,且点积还蕴含着向量之间的相似性,有利于我们学习单词之间的相关性。因此
$$F((w_{i}-w_{j})^\top w_{k})=\frac{P_{ik}}{P_{jk}}.$$如前面所说,三个单词的位置是可以互相转换的,所以函数 \(F\) 应是一个同态,即
$$F((w_{i}-w_{j})^\top w_{k})=\frac{F(w_{i}^\top w_{k})}{F(w_{j}^\top w_{k})}=\frac{P_{ik}}{P_{jk}}.$$可以用指数函数将差和商联系起来,令 \(F=\exp\),因此
$$w_{i}^\top w_{k}=\log(P_{ik})=\log(X_{ik})-\log(X_{i}).$$由于单词位置是可以互相转换的(对称的),并且 \(\log(X_{i})\) 和 \(k\) 相互独立,因此引入两个偏置项来保证这种对称性:
$$w_{i}^\top w_{k}+b_{i}+b_{k}=\log(X_{ik}).$$原论文使用加权最小二乘回归拟合上述模型,损失函数为:
$$J = \sum_{i,j=1}^{V} f\left( X_{ij} \right) \left( w_i^T \tilde{w}_j + b_i + \tilde{b}_j - \log X_{ij} \right)^2,$$其中,\(V\) 是词库大小。\(f(X_{ij})\) 是权重函数,满足如下几个性质: `
-
\(f(0)=0\),即两个词没有共同出现过,权重为 0。
-
\(f(x)\) 是非减函数,因为两个词共同出现次数越多,权重应越大。
-
\(f(x)\) 对于频繁出现的单词,给予较小的权重。如“the”、“a”这类词,它们并不能反映很多的信息。
基于上述几个性质,GloVe 定义 \(f(x)\) 为:
$$f(x) = \begin{cases} (x/x_{\max})^\alpha & \text{if } x < x_{\max}, \\ 1 & \text{otherwise}. \quad \end{cases}$$FastText
Word2Vec 和 GLoVe 有两个共同的缺点:
-
OOV:这两个方法都是得到各个单词的向量表示,如果遇到语料库中没有的单词,则无法构造出其向量表示。
-
Morphology:参数都是根据上下文学习,play、playing 和 played 这些意义非常接近的单词参数不共享。
为此,FastText 考虑子词的信息,将字符级别的 n-gram 和 Word2Vec 进行结合。每个单词添加前后尖括号表示起始和末尾,如“eating”\(\rightarrow\)“<eating>”,它的字符级别的 n-grams 如下:
| Word | n | Character n-grams |
|---|---|---|
| <eating> | 3 | <ea, eat, ati, tin, ing, ng> |
| <eating> | 4 | <eat, eati, atin, ting, ing> |
| <eating> | 5 | <eati, eatin, ating, ting> |
FastText 采用 Skip-gram 模型,并将输入的中心词的向量表示为它所有 n-gram 向量的和,而输出词的向量是它本身。还是以“The quick brown fox jumps over the lazy dog.”为例,训练样本的结构如下:

接下来的训练过程则与 Word2vec 类似。因此 FastText 是 Word2Vec 的改进版本,考虑了每个单词的内部结构,充分使用子词信息,可以有效缓解 OOV 问题。
参考文献
Word2Vec
1.Tomas Mikolov et al. Efficient Estimation of Word Representations in Vector Space [pdf]
2.Tomas Mikolov et al. Distributed Representations of Words and Phrases and their Compositionality [pdf]
3.Chris McCormick. Word2Vec Tutorial - The Skip-Gram Model
4.Chris McCormick. Word2Vec Tutorial Part 2 - Negative Sampling
5.Jay Alammar. The Illustrated Word2vec
GloVe
6.Jeffrey Pennington et al. GloVe: Global Vectors for Word Representation [pdf]
FastText
7.Amit Chaudhary. A Visual Guide to FastText Word Embeddings
8.Piotr Bojanowski et al. Enriching Word Vectors with Subword Information [pdf]